А вот кому гауссов? (комментировать лучше у автора)

[taki_net]

Оригинал взят у podmoskovnik в А вот кому гауссов? (комментировать лучше у автора)

Originally posted by eugenyboger at Традиционные графики по выборам мэра Москвы 8 сентября 2013 г.

Последние данные ЦИК по 3595 участкам.

1. Самая интересная картинка: гистограмма распределения процента за Собянина, взвешенная на размер участка (графа 1 в протоколе). Если совсем просто, то для каждого значения процента за Собянина (ось X) по оси Y отложена общее списочное количество избирателей на участках, на которых получился соответствующий результат. Такое взвешивание позволяет корректно учитывать абсолютное влияние возможных фальсификаций, а так же исключить артефакты деления от маленьких чисел.
   Процент здесь и далее посчитан стандартным способом, используя общее количество найденных в урнах бюллетеней.
   
   Фит распределением гаусса.
   
   
   
   Выводы: гистограмма процента за Собянина просто прекрасно описывается нормальным распределением. Исключение составляет участок у правого хвоста распределения, где можно заметить превышение уровня над ожидаемым распределением. Т.к. гаусс - распределение симметричное и данные им неплохо описываются, то наиболее вероятное значение процента за Собянина приблизительно соответствует искомому среднему.
   
   Среднее значение модели в правом верхнем углу графика, находится в районе 51.0%. Значение очень незначительно меняется (сотые процента), если выкидывать из рассмотрения данные в районе подозрительного выброса справа (напомню, что это не означает исключения комиссий с большим процентом за Собянина из подсчёта результатов, они лишь не участвуют в построении модели, которая неплохо строится и по остальным данным).
   
   Объём фальсификаций в подсчёте итогов голосования, если они встречались локально, не превышает 0.5% по предварительной оценке.
   



2. Взвешенное распределение явки, фит гауссом.
   
   
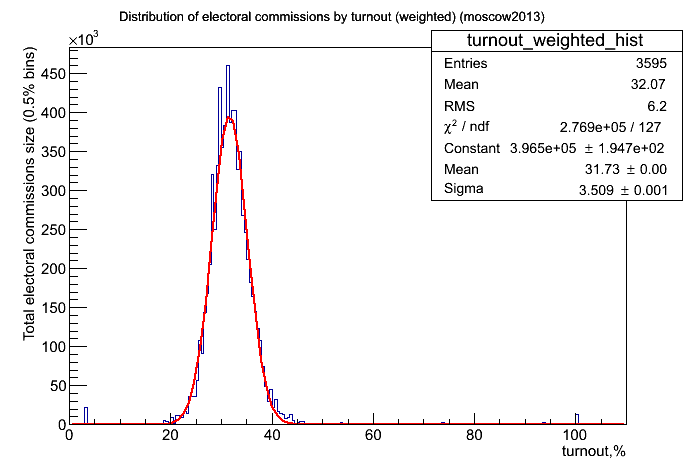
   Почти то же самое: незначительно превышение справа на хвосте.
   



3. Двумерная взвешенная гисторамма: процент за Собянина от явки.
   
   
   
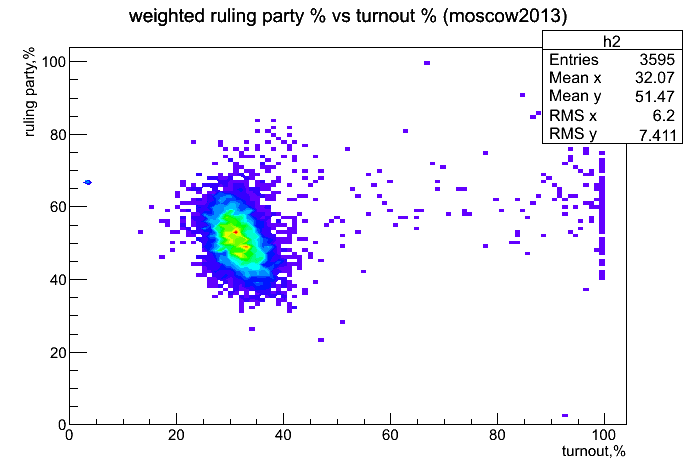
   Выводы: выглядит прилично, видна отрицательная корреляция процента за Собянина и явки. Чем больше приходило людей на участки, тем хуже был результат Собянина . Что подтверждает печальный факт: не все противники действующей власти были мобилизованы на выборы.
   Коэффициент корреляции в центральном регионе: -0.28.
   
   


4. Фит слайсов (оно же profile) предыдущей картинки. Простыми словами: для каждого значения явки была построена гистограмма распределения процента голосов за Собянина. Эта гисторамма была зафитирована распределением гаусса. Среднее значение, получившееся в такого фита, отложено по оси Y.
   
   Красная линия - фит центрального региона прямой. Коэффициенты справа.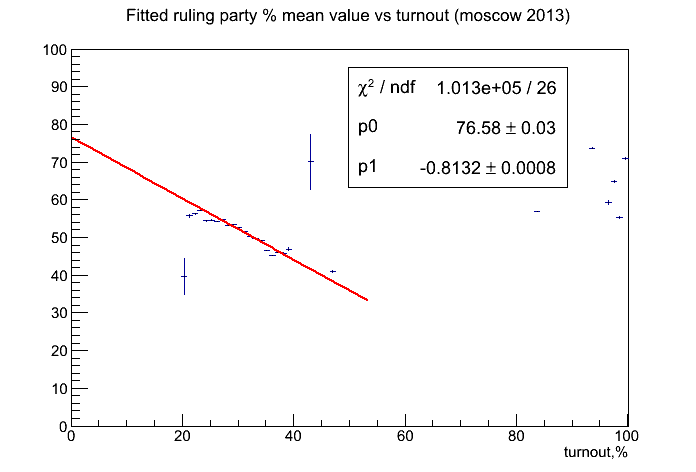
   
   Выводы: Угловой коэффициент -0.8 как бы намекает на масштаб эффекта.
   

Все данные, скрипты и картинки в репозитории https://github.com/evgeny-boger/rus-elections-stats/

Важный вывод из всего этого: товарищи эксперты, утверждавшие, что нормальное распределение не применимо для описания выборов вообще, российских выборов, московских выборов и т.д. очевидно окончательно оказались неправы. Именно так должны выглядеть графики для честных результатов голосования, хотя бы в масштабе одного региона. Стоит ли говорить, что на президентских и думских выборах всё выглядело немного не так.

Comments

[francis-drake.livejournal.com]

> Чем больше приходило людей на участки, тем хуже был результат Собянина. Что подтверждает печальный факт: не все противники действующей власти были мобилизованы на выборы.
Не может ли это означать, напротив, что "противники действующей власти" не были распределены по городу равномерно?

[taki-net.livejournal.com]

Podmoskovnik то же самое говорит.

[zepete.livejournal.com]

Было бы так, то гистограммы на распределение Гаусса не похожи были.

[stzozo.livejournal.com]

Следует заметить, что на нечестных выборах тоже может быть гауссово распределение.
Зависит от того, как фальсифицировать.

[imfromjasenevo.livejournal.com]

конечно, просто сложней фальсифицировать, чтобы выглядело чисто.
Нужно вбрасывать с умом и максимально равномерно по участкам.

[stzozo.livejournal.com]

Не так уж и сложней.
Можно, например, вбрасывать не равномерно, просто неорганизованно.
Гауссиана плюс гауссиана равно почти гауссиана.

[imfromjasenevo.livejournal.com]

чтобы вбрасывать неравномерно по гауссиане требуется строгая организация, что не просто.

[stzozo.livejournal.com]

Наоборот, отсутствие организации сделает вбросы случайными.

[imfromjasenevo.livejournal.com]

нет, отсутствие организации сделает вбросы видными, вбрасывать случайно человек не может ,не применяя рандомизатор типа хотя бы игральных костей.

[stzozo.livejournal.com]

Голосуют люди тоже неслучайно, без всякого рандомизатора.
Но в сумме получается гауссиана.

[imfromjasenevo.livejournal.com]

если число твоих сторонников достаточно велико, то ты получишь гауссиану, да.
но тогда ты выиграешь и честным путем.

[stzozo.livejournal.com]

У проигравших кандидатов тоже получается гауссиана.

[imfromjasenevo.livejournal.com]

это разумно, но все равно
дать приказ вмешаться, но при этом сделать это случайно очень сложно, каким образом задать дисперсию фальсификаций?
все равно будут ретивые, которые впишут сто?
а если сделать отсечку, то будет пик на ней.

[stzozo.livejournal.com]

Возможно, Вы правы.

[imfromjasenevo.livejournal.com]

т.е. гаусс может и будет (если еще удастся вбрасывать при бдительных наблюдателей),
но вбрасывать мало нельзя не будет эффекта, а много сложно и надо еще подделывать явку, а если разрешить вольницу, то разброс станет очень большим - появятся странный хвост
Если просто заниматься приписками, то все равно будут проблем с протоколами и последними и предпоследними цифрами, которые тоже ловятся.

[stzozo.livejournal.com]

Ну проколы с последними цифрами - это совсем топорная халтура.

[vedroid.livejournal.com]

Ну если плюс заменить на помножить, то это даже верно.

[stzozo.livejournal.com]

Именно плюс.
Но здесь ведь речь про горизонтальный плюс.
Если мы вбрасываем - то меняется количество голосов на каждом участке, а не появляются новые участки, на которых виден только вброс.

[vedroid.livejournal.com]

"горизонтальный плюс"

[stzozo.livejournal.com]

Обычный, вертикальный плюс - это f(x) = f1(x) + f2(x). Он нам здесь ни к чему.
Здесь нужно сделать другое: взять случайную величину, распределенную по первому графику, добавить величину, распределенную по второму графику, и нарисовать график получившейся случайной величины.

[fortness90.myopenid.com (from livejournal.com)]

>Гауссиана плюс гауссиана равно почти гауссиана.

Какой шикарный бред ...

[stzozo.livejournal.com]

Да, я наврал, получается ровно гауссиана.
Если сложить два гауссовых распределения - получается гауссово распределение со средним - суммой средних, и дисперсией - суммой дисперсий.

[vedroid.livejournal.com]

Это верно для независимых случайных величин, а не для распределений.

[stzozo.livejournal.com]

Мы же и складываем независимые случайные величины и получаем распределение их суммы.

[idelsong.livejournal.com]

Гауссово распределение связано с отсутствием в Москве этнически, религиозно или идеологически гомогенных районов. В Израиле, где такие районы есть (харедимские, религиозные, кибуцы, арабские и друзские деревни) - распределение очень далеко от гауссова. Подозреваю, что в Нью Йорке тоже.

[taki-net.livejournal.com]

На самом деле есть стат. инструменты, которые работают и в этих условиях. Но да, в мегаполисе все проще.